Details
Due date
This assignment is due on Monday, May. 20th, at 11:30 PM.
Coverage
This assignment covers the material up to Week 7, focusing on writing and using classes (OOP) in Python.
Thank you to Adam Abbas for his work on helping create this CS 1 assignment in 22fa, and TAs since who have helped iterate!
Overview
In this assignment, you'll explore the concepts we've learned about OOP (object-oriented programming) and apply them to a really cool physical concept - crystals! As you might have learned in chemistry, atoms can align themselves into a "lattice" (which is just a fancy word for the 3D arrangement of our atoms). You'll finish developing a basic Python class representation of a lattice, and implement some of the associated methods.
Specifically, you'll be finishing the implementation of two classes to represent
crystal lattices, essentially a collection of “atoms”. Atoms themselves are
a class; a basic one only containing a string representing the kind of element
the atom represents (e.g. 'Fe' for Iron), and the (x, y, z) coordinate location
of that atom.
By the end of the assignment, you'll be able to generate crystal lattice data in a standard .xyz file format to visualize your structures! The viewer you will be using is http://calistry.org/calculate/xyzviewer where you should be able to see the location of each of your atoms. Note: If you have any issues with this viewer rendering in your browser, try either 1) a different browser, 2) a different browser account if you're using a Caltech account, or 3) an alternative viewer called mol* (https://molstar.org/viewer/) which we found for 23sp with a nice suite of extra features but limited student testing. Students with CAD background may find this new tool especially interesting!
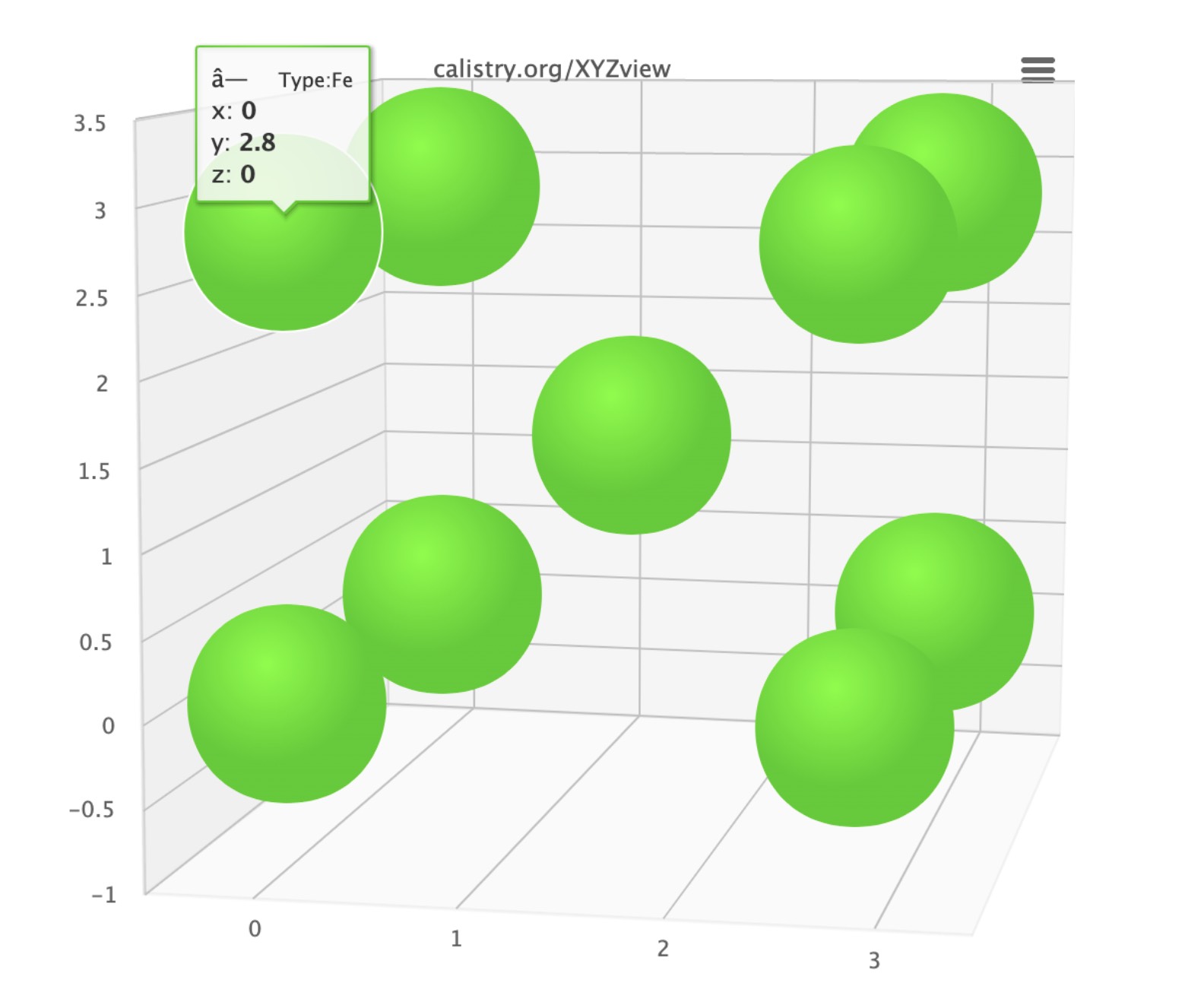
Important: this set may look lengthy, but its length comes from a lot of context/diagrams/example code supporting it. Most of the methods are fairly short (many no more than 5 lines) and the actual work should be consistent with other MPs (estimated 3-4 hours).
What to hand in
You will be submitting 3 files to CodePost for this assignment:
atom.py(Part A)lattice.py(Part B-C)lattice_client.py(Part D)
If you choose to try your hand at the optional features, make a copy of any extended Part A-D files so that your Part A-D solutions still meet the requirements. You can submit any extensions as an additional file.
Below is a summary of the tasks you'll complete; anything in [X] indicates an average estimate of minutes you should expect to take. As always, you should also make sure to test your code iteratively to avoid challenges pin-pointing where a bug occurs.
You should also expect to take up to 15-20 minutes to ensure your
formatting follows PEP8 conventions (use pycodestyle as usual)
and that docstrings are complete (we have provided some docstrings
for you, including all of Part C-D docstrings, aside from the __init__ constructor docstring you'll finish in C.3.).
Part A: Reviewing and Finishing Atom docstrings [10]
Part B: Implementing simple CubicLattice methods
- B.1.
__init__constructor [10] - B.2.
get_lattice_parameter[2] - B.3.
get_cell_volume[2] - B.4.
get_unique_elements[10] - B.5.
get_number_atoms[10-15] - B.6.
get_inverted_cell[20]
Part C: Adding CubicLattice Support for Importing and Exporting .xyz Crystal Data
- C.1.
as_xyz[15] - C.2.
write_to_xyz[5] - C.3. Supporting
in_filenamedefault argument to__init__constructor [15, 10]
Part D: Writing 3 Functions to create 3 different types of CubicLattice structures
- D.1.
create_SC[5] - D.2.
create_BCC[5-10] - D.3.
create_FCC[10-15]
Useful Terminology
- Crystal Lattice: "the symmetrical three-dimensional arrangement of atoms in a crystal" (source: Wikipedia)
- Unit Cell: the "building block" of a crystal, a unit cell is the simplest arrangement of atoms which can be repeated to form the entire crystal. While a unit cell itself is a crystal lattice, a given lattice may not be a unit cell, as it may not represent a portion of a larger crystal.
- Lattice Parameter: the side lengths of the crystal's unit cell. A single lattice can have up to 3 lattice parameters (denoted a, b, and c), which are usually associated with three angles (denoted α, β, γ). Note that the lattice parameter is sometimes referred to as a lattice constant, but we will use the term lattice parameter here.
For more details about crystal lattices and unit cells, this is a summary.
Supporting Files
We have provided you starter.zip code for the three files you will finish.
atom.pylattice.pylattice_client.py
Test Files
We have also provided a test suite for your solutions, which tests the full import/export
functionality of your CubicLatticeand lattice_client.py functions.
You can download the test files here and refer to the provided test instructions.txt (you will copy your solutions into this directory
to test your code). Note that when tests compare your output files with the expected output (see test_files/, we have added some leniency on int vs. float (ints are standardized to their
float counterpart) to support lattices with either type for Atom coordinates. We may add a smaller test program for iterative testing soon (to help you pinpoint where a bug might be
occurring), but it will use the examples given in this spec.
Part A (Warm-Up): Understanding a Simple Atom Class
[10]
To get started, you'll review the provided Atom class (in atom.py).
This is a very basic class, representing a single Atom with an element
(e.g. 'Fe' is the expected element for "Iron") and (x, y, z) coordinates.
This class provides the required __init__ constructor that every Python class
should have, followed by a __str__ method.
Remember that __str__ is required to support more readable string
representations, and is used when passing in an object of
the class to str(...) or print(...) (or when
passed in a f'...' format string).
You can see these use cases Python provides for a class with a __str__
method in the examples below.
>>> from atom import Atom
>>> fe0 = Atom('Fe', (0.0, 0.0, 0.0))
>>> fe1 = Atom('Fe', (.5, .5, .5))
>>> na0 = Atom('Na', (0.0, 0.0, 0.0))
>>> k0 = Atom('K', (2.5, 2.5, 2.5))
>>> (x, y, z) = fe0.get_coordinates()
>>> print(f'{fe0.element} with coords ({x}, {y}, {z})')
Fe with coords (0.0, 0.0, 0.0)
>>> str(fe0)
'Fe 0.0 0.0 0.0'
>>> print(fe0)
Fe 0.0 0.0 0.0
>>> print(na0)
Na 0.0 0.0 0.0
>>> print(k0)
K 2.5 2.5 0.0
>>> print(f'The .xyz format for fe1 is: {fe1}')
The .xyz format for fe1 is: Fe 0.5 0.5 0.5
While it may not be obvious yet, the string representation we have chosen for an
Atom will be very useful in Part C, where you will write functionality
in CubicLattice to write (export) a crystal structure to an .xyz file
(which includes Atom data for each atom in a crystal, represented with
the standard xyz form the Atom's __str__ method follows).
In general, we don't want a string representation to be dependent on some client
program/class, but the xyz format is a common convention for representing Atom's
of a certain element and at an (x, y, z) coordinate.
The class also provides a single getter method called get_coordinates.
This returns a tuple of the (x, y, z) coordinates of the Atom that
were set upon construction.
>>> # continued from above
>>> (x, y, z) = fe0.get_coordinates()
>>> print(f'{fe0.element} with coords ({x}, {y}, {z})')
Fe with coords (0.0, 0.0, 0.0)
>>> (x, y, z) = k0.get_coordinates()
>>> print(f'{k0.element} with coords ({x}, {y}, {z})')
K with coords (2.5, 2.5, 0.0)
Observe that the Atom class has no methods to update the state.
This is appropriate for the Atom class, since an Atom
fundamentally doesn't have any state that makes sense to update.
As discussed in lectures and the readings, some classes do make sense to support state
modification (e.g. a Student's add_course method) and some don't.
We have provided you the following docstrings as another reference for
getting started with documentation conventions for a Python class,
which you should refer to when documenting lattice.py:
- The program overview (you should replace your name); because the
atom.pyfile just defines anAtomclass, the overview simply summarizes that; thelattice.pyprogram has a few functions below theCubicLatticeclass definition, so that program overview would focus on summarizing the overall functionality offered inlattice.py(as usual, without implementation details) -
The class docstring, just under the
class Atom:line -
The
__init__constructor docstring to help serve as reference for method docstrings, as well as an example of documentation for a raised error (specific errors that could be raised by a method should be specified, such as aValueErrorin this case). Note that we don't refer to theselfparameter in the method comment, which is important to keep in mind when you write class method docstrings. Only the arguments a user of the class would pass when calling a method (such as the constructor) should be specified.
You saw a few examples of constructing simple Atom objects above. Note that the constructor supports argument-validation, raising a ValueError if an invalid lparam is given. You can see this behavior below:
>>> # continued from above
>>> # An atom's coordinates must have exactly 3 values in a tuple
>>> invalid_fe = Atom('Fe', (0.0, 0.0, 0.0, 0.0))
ValueError: coordinates must be a 3-element tuple representing (x, y, z) Atom coordinates.
You aren't expected to handle this in any special way right now, but it's important for clients to know this precondition when using the class.
Part A Exercises
- A.1. Write a docstring for the
get_coordinatesmethod. - A.2. Write a docstring for the
__str__method.
Again, we have provided the implementation for these methods for you, which should be unchanged.
You can test your docstrings using the help(...) function.
This prints out the class docstring; what you see printed here comes from the starting documentation.
Observe where the program vs. class vs. __init__ method docstrings
are located in the generated documentation. Also observe what Python's help
function will include by default when printing the class docstrings. Once you add the two other docstrings, they would be added to the output.
>>> from atom import Atom >>> help(Atom) Help on class Atom in module atom: class Atom(builtins.object) | Atom(element, coordinates) | | Simple class representation of an atom. Contains information on the | represented element and (x, y, z) location of the atom in a lattice. | | Attributes: | - element (str): element name of Atom, e.g. 'Fe' | - coordinates (float, float, float): (x, y, z) coordinates of Atom | | Methods defined here: | | __init__(self, element, coordinates) | Constructs an Atom instance representing the `element` with | the specified (x, y, z) `coordinates`. While not recommended, | negative coordinate values are supported, as long as coordinates | are passed with exactly 3 values. | | Arguments | element (str): Name of element (e.g. 'Fe') | coordinates (tup): tuple holding (x, y, z) coordinates | (e.g. (0.0, 0.5, 0.5)) | | Raises: | ValueError if coordinates is not a 3-element tuple. | | get_coordinates(self) | A.1. TODO docstring | | __str__(self) | A.2. TODO docstring | | ... # rest omitted >>> help(Atom.get_coordinates) # prints out the Atom's get_coordinates method >>> # clients of your Atom class should see something useful here
Part B: Geometry of Cubic Lattices
The second class you'll be working with is the CubicLattice class, the most basic kind of lattice.
As the name suggests, cubic lattices have their atoms placed around a cube. That means that their
lattice parameters are all equal to each other, and the angles of the unit cell are all 90 degrees.
Image source Chemistry Dictionary and Glossary (periodni.com)
We will only work with CubicLattics in this assignment, though you are welcome to extend your implementations to support other types of lattice structures in the optional Extra Features section we've included at the end of this document.
These tasks will reference CubicLattice methods in the lattice.py file.
1. The CubicLattice __init__ Constructor
[10]
As with all classes, we'll want to start with the constructor. For CubicLattice, we support the following arguments:
- The lattice parameter for the crystal, called
lparam. - A list of
Atoms calledatoms
We're only working with cubic structures, so there is only one lattice parameter (a = b = c); we represent it as lparam to simplify; both class fields (attributes) should match these names.
Note: If you choose to extend your program to support other types of crystal lattice classes, where lattice parameters are not equivalent, you'd want to keep track of each a, b, and c instead of a single lparam in those other lattice classes.
You'll note that the starting code has two optional arguments after the lattice parameter:
atoms=[]in_filename=None
As you've already experienced quite a bit in Matplotlib, optional arguments
are very useful to support different functionality in a class without having to add multiple versions
of a method. Any parameter in the form <name>=<default value> is defined as an optional parameter in Python,
holding the specified default value if the client does not pass a specific value for it.
Here, we set the defaults to atoms to [] and in_filename to None, which means that if the client only
passes the required lparam argument, a CubicLattice object will be created with no atoms and from no input file data.
In B.1., you'll ignore in_filename=None for now; just assume that no in_filename is passed. You don't need to do anything special for atoms; whether or not it was passed (e.g. a list of Atoms or []),
just set the atoms attribute to the passed atoms argument.
So with all that said, the constructor is relatively simple for this exercise:
- First, check if
lparamis valid; alparam<= 0 is an invalid representation of a cube. If a client passes an invalidlparam, raise aValueErrorwith the message "lparam must be positive." (refer to the providedAtomconstructor, which raised aValueErrorfor an invalid tuple argument) - Otherwise, initialize the
lparamand atoms attributes for the newCubicLattices
You do not need to handle any cases where two atoms are at the same location or that atoms are
within the bounds of an lparam^3 cube (in practice, we would, but
we are keeping things simple for the scope of MP6).
Here are some examples of expected behavior for B.1.:
>>> from atom import Atom
>>> from lattice import CubicLattice
>>> fe0 = Atom('Fe', (0.0, 0.0, 0.0))
>>> fe1 = Atom('Fe', (.5, .5, .5))
>>> na0 = Atom('Na', (0.0, 0.0, 0.0))
>>> k0 = Atom('K', (2.5, 2.5, 0.0))
>>> ex1 = CubicLattice(1.0, [fe0])
>>> ex2 = CubicLattice(2.0, [fe0])
>>> ex3 = CubicLattice(1.0, [fe0, fe1, na0, k0])
>>> ex3
<lattice.CubicLattice object at 0x1031fa410>
>>> for atom in ex1.atoms:
... print(atom) # uses Atom's __str__ method internally
...
Fe 0.0 0.0 0.0
>>> for atom in ex3.atoms:
... print(atom)
...
Fe 0.0 0.0 0.0
Fe 0.5 0.5 0.5
Na 0.0 0.0 0.0
K 2.5 2.5 0.0
>>> ex1.lparam
1
>>> ex2.lparam
2
>>> ex4 = CubicLattice(1) # atoms defaults to []
>>> ex4.atoms # atoms defaults to [] here
[]
>>> invalid_lattice = CubicLattice(-1, [fe0])
ValueError: lparam must be positive.
>>> invalid_lattice = CubicLattice(0, [fe0])
ValueError: lparam must be positive.
Once you finish, write an appropriate docstring for this constructor (examples of class and method documentation
was covered in lecture, and you can refer to Atom's constructor for another example). For B.1., ignore the in_filename parameter
when writing the docstring for now; you'll account for that later.
Your solution should be about 4 lines after the docstring.
Note: In Part C.1., you will finish this constructor to add support
for the optional in_filename parameter.
Once you have the constructor done, you'll implement some basic methods in the CubicLattice class.
Reminder: At this point in the assignment, we want to remind you that you should not be making any
direct calls to __init__ or __str__; these are only used for defining
these special methods so that other code using the class can use the constructor (the class name) and the str
function passing in an instance of some class with a defined __str__ method. Refer to lectures for
discussion/more examples of this if needed.
2. get_lattice_parameter
[2]
This method should return the lattice parameter of the crystal lattice (for a cubic lattice with the parameter representing the length of each face, that simply represents the shared a = b = c value). The expected solution has 1 line after the docstring.
Examples are provided below:
>>> from atom import Atom
>>> from lattice import CubicLattice
>>> ex_crystal = CubicLattice(1, atoms=[Atom('Au', (0.0, 0.0, 0.0)), Atom('Pt', (.5, .5, .5))])
>>> ex_crystal.get_lattice_parameter()
1
3. get_cell_volume
[2]
This method should return the volume of the cubic lattice (this is just based on the lattice parameters, and does not take into account the relevant atoms). Remember that the standard unit we are using is the Angstrom, so volume is represented as Angstrom^3. The expected solution has 1 line after the docstring.
Examples are provided below:
>>> from atom import Atom
>>> from lattice import CubicLattice
>>> ex1 = CubicLattice(1.0, atoms=[Atom('Au', (0.0, 0.0, 0.0))])
>>> ex1.get_cell_volume()
1.0
>>> ex2 = CubicLattice(1.0, atoms=[Atom('Au', (0.0, 0.0, 0.0)), Atom('Fe', (1.0, 1.0, 1.0))])
>>> ex2.get_cell_volume() # Number of Atoms doesn't change the cube lattice volume
1.0
>>> ex3 = CubicLattice(1.5, atoms=[Atom('Au', (0.0, 0.0, 0.0))])
>>> ex3.get_cell_volume()
3.375 # 1.5 * 1.5 * 1.5
>>> ex4 = CubicLattice(2.0, atoms=[Atom('Au', (0.0, 0.0, 0.0))])
>>> ex4.get_cell_volume()
8.0
4. get_unique_elements
[10]
This method should return a list of all of the unique elements contained in the lattice,
where each element in the list is a string element name that comes from an Atom
in the lattice's atoms collection.
Hint: You'll need a loop over self.atoms, and add each unique element string
to the result list no more than once before returning the result.
Our solution has 5 lines of code after the docstring.
>>> from atom import Atom
>>> from lattice import CubicLattice
>>> fe0 = Atom('Fe', (0.0, 0.0, 0.0))
>>> fe1 = Atom('Fe', (.5, .5, .5))
>>> na0 = Atom('Na', (0.0, 0.0, 0.0))
>>> k0 = Atom('K', (2.5, 2.5, 0.0))
>>> ex0 = CubicLattice(1, [fe0, na0, fe1, k0])
>>> ex0.get_unique_elements()
['Fe', 'Na', 'K']
>>> empty_crystal = CubicLattice(1.0)
>>> empty_crystal.get_unique_elements()
[] # atoms defaults to []
5. get_number_atoms and 6. get_inverted_cell
The next two methods will support functionality specific to Atoms and their positions
within our cubic crystal lattice. We often refer to a crystal's "unit cell" -
the smallest possible repeating lattice to form our crystal. The emphasis here is on
"repeating", since crystals are made up of an enormous number of these lattice units.
Why are we emphasizing this? Because we want to count the number of atoms inside a single lattice, but atoms
usually are shared between adjacent lattices. A useful diagram is provided below, which will also be a useful reference
in Part D.
Note: Each of the three examples represents a single unit cell, but remember that a crystal structure is likely composed of repeating cells, as depicted in the Overview diagram.
The first cubic cell shown below has 8 “corner atoms”; each is 1/8 of the atom it belongs to.
The second cubic cell has 1 “center atom” (1/1 of the atom); there also happen to be 8 corner atoms, which will be relevant when implementing create_BCC in Part D.2.
The last cubic cell has 6 “face” atoms”, each being 1/2 of the atom it belongs to. There also happen to be 8 corner atoms in this diagram.
Corner vs. Center vs. Face Atoms in a Unit Cell
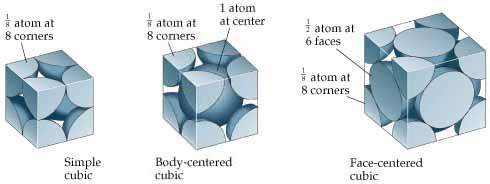
In this project, we're curious about the relative number of atoms in the unit cell. As you see above, depending on where on
the lattice the atom is, it may be counted as only a fraction of an atom,
instead of a whole atom. For example, take an atom on the corner of the lattice
cube. When repeated, that atom can be found in 8 different cells
(a 4x4 lattice comprised of 8 lattices, all having 1/8 of a corner Atom.
That means that any atom located at a cube's corner should be counted as an eighth.
Similar logic applies to other positions.
To keep the following exercises simple, we will only focus on three atom positions:
- Atoms at the corner of a lattice (1/8)
- Atoms at the center of a lattice (1, the entire atom)
- Atoms at the center of a face of a lattice (1/2, half the atom)
With that in mind, our goal is to implement the following B.5. and B.6. CubicLattice methods.
In terms of the implementation, you'll have to do some careful thinking about the role of Atom objects inside a
CubicLattice object, so expect these next 2 methods to require
more time than the methods you just wrote.
5. get_number_atoms
[10]
This method should return the collected number of atoms in a given crystal lattice (as a float),
using the adjusted counting discussed above. At the bottom of lattice.py,
just after the end of the CubicLattice class definition, we have given
you 3 helper functions is_corner, is_cell_center,
and is_face_center, which return booleans corresponding to whether the given (x, y, z)
coordinates are at the respective location in a cube having the passed length.
These three functions generalize to any 3D cube structure, which is why we define them as functions not unique only to
a CubicLattice structure). We could factor them out into a crystal_utils.py
program, but decided to keep them in lattice.py to simplify things.
For the examples in the diagram above, a lattice represented as the first unit cell would have 1 atom total; the second cell would correspond to 1 + (1/8 * 8) = 2 atoms, and the third would correspond to (1/2 * 6) + (1/8 * 8) = 4 atoms.
Below are some example calls of get_number_atoms() for different CubicLattices.
Note that CubicLattice supports int or float
lparam values, but the returned value for this method should always be a float. Additional examples can be found in the provided
test_isolated_mp6_ab.py tests.
>>> from atom import Atom
>>> from lattice import * # import the CubicLattice and 3 helper functions
>>> is_corner((0.0, 0.0, 0.0), 1)
True
>>> fe0 = Atom('Fe', (0.0, 0.0, 0.0))
>>> ex0 = CubicLattice(1, [fe0]) # (0.0, 0.0, 0.0) is a corner
>>> ex0.get_number_atoms()
0.125 # 1/8
>>> is_corner((.5, .5, .5), 1)
False
>>> is_cell_center((.5, .5, .5), 1)
True
>>> fe1 = Atom('Fe', (.5, .5, .5))
>>> ex1 = CubicLattice(1, [fe1]) # (.5, .5, .5) with a lattice parameter of 1 is the center
>>> ex1.get_number_atoms()
1.0 # 1/1
>>> fe2 = Atom('Fe', (.5, .5, 0.0))
>>> is_face_center((.5, .5, 0.0), 1)
True
>>> ex2 = CubicLattice(1, [fe2]) # (.5, .5, 0.0) with a lattice parameter of 1 is on a face
>>> ex2.get_number_atoms()
0.5 # 1/2
>>> is_cell_center((.5, .5, .5), 1)
True
>>> na0 = Atom('Na', (0.0, 0.0, 0.0))
>>> ex3 = CubicLattice(1, [fe1, na0]) # 1 center atom + 1 corner atom
>>> ex3.get_number_atoms()
1.125 # 1 + 1/8
>>> fe3 = Atom('Fe', (1.0, 1.0, 1.0))
>>> na1 = Atom('Na', (1.0, 0.0, 0.0))
>>> ex4 = CubicLattice(1, [fe0, fe3, na1]) # 3 corners
>>> ex4.get_number_atoms()
0.375 # 1/8 + 1/8 + 1/8
>>> ex5 = CubicLattice(3, [fe0]) # fe0 is corner (0.0, 0.0, 0.0)
>>> ex5.get_number_atoms()
0.125 # 1/8, same as ex0
>>> al0 = Atom('Al', (3.0, 3.0, 3.0))
>>> is_corner((3.0, 3.0, 3.0), 1.0)
False
>>> is_corner((3.0, 3.0, 3.0), 3.0)
True
>>> al1 = Atom('Al', (3.0, 1.5, 3.0))
>>> al2 = Atom('Al', (3.0, 3.0, 1.5))
>>> is_corner((3.0, 1.5, 3.0), 3)
False
>>> is_face_center((3.0, 1.5, 3.0), 3)
True
>>> is_face_center((3.0, 3.0, 1.5), 3)
True
>>> ex6 = CubicLattice(3.0, [al0, al1])
>>> ex6.get_number_atoms()
0.625 # 1/8 + 1/2
>>> ex7 = CubicLattice(3.0, [al0, al1, al2])
>>> ex7.get_number_atoms()
1.125 # 1/8 + 1/2 + 1/2
>>> al3 = Atom('Al', (1.5, 1.5, 1.5))
>>> ex8 = CubicLattice(3.0, [al0, al1, al2, al3])
>>> ex8.get_number_atoms()
2.125 # 1/8 + 1/2 + 1/2 + 1
6. get_inverted_cell
This method should return a new CubicLattice, where all the atoms
are flipped around the center of the cube. The CubicLattice instance this method
is called on should be unchanged as a result of calling this method.
Again, you do not need to handle any cases where two atoms are at the same location (in practice, we would, but
we are keeping things simple for the scope of MP6).
Note: Expect this method to be one of the trickier ones in this assignment.
This method requires a good understanding of state and methods (the original CubicLattice
should not be modified!), as well as a careful approach to the pseudocode of how to invert a cube
structure. We strongly recommend you to write pseudocode before implementing this code,
starting with drawing out an example for a basic CubicLattice and the expected
properties of the returned inverted lattice. You are welcome to continue on to Parts C and D and
return to this (required) exercise later, as it is not required for those parts.
Note that so far, all of these methods only depend on the lattice parameter! The actual kinds of atoms in our crystal won't change the result of any of these methods. We'll change that in the next section, where we'll look at some other interesting properties of a lattice.
>>> from atom import Atom
>>> from lattice import CubicLattice
>>> fe000 = Atom('Fe', (0.0, 0.0, 0.0))
>>> fe111 = Atom('Fe', (1.0, 1.0, 1.0))
>>> na100 = Atom('Na', (1.0, 0.0, 0.0))
>>> ex4 = CubicLattice(1, [fe000, fe111, na100]) # 3 corners
>>> for atom in ex4.atoms:
... print(atom)
...
Fe 0.0 0.0 0.0
Fe 1.0 1.0 1.0
Na 1.0 0.0 0.0
>>> ex4_inverted = ex4.get_inverted_cell()
>>> for atom in ex4_inverted.atoms:
... print(atom)
...
Fe 1.0 1.0 1.0
Fe 0.0 0.0 0.0
Na 0.0 1.0 1.0
>>> for atom in ex4.atoms: # double-check that ex4 is not modified
... print(atom)
...
Fe 0.0 0.0 0.0
Fe 1.0 1.0 1.0
Na 1.0 0.0 0.0
>>> fe222 = Atom('Fe', (2.0, 2.0, 2.0))
>>> na200 = Atom('Na', (2.0, 0.0, 0.0))
>>> ex5 = CubicLattice(2, [fe000, fe222, na200]) # changing lattice parameter
>>> for atom in ex5.atoms:
... print(atom)
...
Fe 0.0 0.0 0.0
Fe 2.0 2.0 2.0
Na 2.0 0.0 0.0
>>> ex5_inverted = ex5.get_inverted_cell()
>>> for atom in ex5_inverted.atoms:
... print(atom)
...
Fe 2.0 2.0 2.0
Fe 0.0 0.0 0.0
Na 0.0 2.0 2.0
Part C: Importing and Exporting Crystal Data
It's quite feasible to imagine that we might want to use our CubicLattice class to represent
real data, and as such would want to be able to share it with other scientists and
software developers! To that end, we'll be implementing two related features:
exporting our CubicLattice to a file, and reading a file to create a
CubicLattice structure. Luckily, we've already learned how to read and write files in Python!
These tasks will reference methods in the lattice.py file.
C.1. XYZ Representation
[15]
We'll be using the convenient .xyz file format for crystals. The overall
format is simple: the first line contains the number of atoms, the second line has a “description”
of the structure (we'll just use a specified crystal name), and the
rest of the file contains lines of the following format:
element x_coordinate y_coordinate z_coordinate.
Finish as_xyz to return a string representation of the CubicLattice
in the specified XYZ format, given a passed crystal name. You are not writing any files in
this method, but should return a string in a format that can be written to an .xyz file, with \n
characters at the end of each line (including the last line). For reference, our solution is 5-6 lines,
in addition to some inline comments to clarify the three components written (name, length,
1+ lines of atom data).
Some examples are provided below:
>>> from atom import Atom
>>> from lattice import CubicLattice
>>> fe0 = Atom('Fe', (.5, .5, .5))
>>> na0 = Atom('Na', (0.0, 0.0, 0.0))
>>> ex1 = CubicLattice(1, [fe0, na0])
>>> ex1_xyz = ex1.as_xyz('Fe and Na Crystal')
>>> ex1_xyz
'2\nFe and Na Crystal\nFe 0.5 0.5 0.5\nNa 0.0 0.0 0.0\n'
>>> print(ex1_xyz)
2
Fe and Na Crystal
Fe 0.5 0.5 0.5
Na 0.0 0.0 0.0
>>> print(ex1_xyz.rstrip()) # removes the last \n
2
Fe and Na Crystal
Fe 0.5 0.5 0.5
Na 0.0 0.0 0.0
C.2. Exporting with write_to_xyz
[5]
Use your as_xyz method to write the crystal (with the specified crystal name)
to a new file named out_filename. This function is short
when you use your other method; ours is 3-4 lines after the docstring.
For example, a call to ex1.write_to_xyz('Fe and Na Example', 'ex1.xyz') would save the output above to a file ex1.xyz.
C.3. Importing with get_atoms_from_xyz and __init__'s in_filename optional parameter
[15, 10]
Now that we have the ability to write .xyz files, it would be great if
we could use those files to create and work with CubicLattice instances!
You may have noticed that we have a default argument in our constructor called
in_filename — this will be used as an alternative to a list of atoms to create a new CubicLattice class.
For more information on how to define default parameters in methods/functions (you've already used them in Matplotlib!), refer to Lecture 21.
To help accomplish this, implement the get_atoms_from_xyz method.
This simply reads an .xyz file, and returns all of the atoms contained in it.
We can then use this method in our constructor, as an equivalent way of assigning the CubicLattice's atoms
list.
After you've implemented get_atoms_from_xyz, modify your __init__
constructor to check for a passed in_filename.
If none is passed, the atoms attribute should be set to the passed
atoms argument, just like you should already have implemented.
Otherwise, populate the CubicLattice's atoms
attribute to be the list of Atoms returned from get_atoms_from_xyz.
Once you're done, update the docstring to specify the behavior of the
constructor with the optional arguments. In addition, add a "Raises:"
section in your docstring to specify that a FileNotFound error is
raised if an invalid (but non-empty) filename is passed.
You should not be raising any errors or using try/except
in this method. We are documenting this edge case for clients so that
they know they should handle the raised error if they pass an invalid
filename, since we choose not to handle an invalid file in any special
way in this class.
You should expect your constructor to be about 4 lines longer after
adding support for this optional in_filename argument,
in addition to a few lines added to your docstring.
Part D: Creating Crystals
It's time to test out the class we've created! In this part, you'll implement
three functions to support functionality to
construct three types of cubic lattices using your finished
CubicLattice class; these are the three representations
you saw in Part B's figure. These functions will be written in the third file,
lattice_client.py and will reference the imported Atom
and CubicLattice classes you'll be constructing (we have provided the starter code for you).
We have started you off with a get_corner_atoms function, which takes an element and an lparam, and returns a list of 8
corner Atoms having that element name and with (x, y, z) coordinates scaled by
lparam using the unit-cube CORNERS constant.
Caveat: This is a simplification of crystal lattices, and in practice, different atoms will have different ionic radii based on the element they represent. You do not need to handle this, but are welcome to add support for ionic radii (e.g. with a CSV or dictionary of atom radii) as an optional feature.
D.1. Creating a "Simple" Cubic Lattice
[5-10]
Finish create_SC to return a CubicLattice
consisting of an Atom at each corner of the crystal
(a "simple" cubic lattice). Each Atom is of the same kind of element.
For reference, our solution adds 3 lines of code, including one that
uses the get_corner_atoms helper function.
>>> from lattice_client import *
>>> fe_unit_corner_atoms = get_corner_atoms('Fe', 1.0)
>>> for atom in fe_unit_corner_atoms:
... print(atom)
...
Fe 0.0 0.0 0.0
Fe 1.0 0.0 0.0
Fe 0.0 1.0 0.0
Fe 0.0 0.0 1.0
Fe 0.0 1.0 1.0
Fe 1.0 0.0 1.0
Fe 1.0 1.0 0.0
Fe 1.0 1.0 1.0
>>> ex_scc = create_SC('Fe', 1.0)
>>> ex_scc
<lattice.CubicLattice object at 0x1005adba0>
>>> ex_scc.lparam
1.0
>>> for atom in ex_scc.atoms:
... print(atom)
...
Fe 0.0 0.0 0.0
Fe 1.0 0.0 0.0
Fe 0.0 1.0 0.0
Fe 0.0 0.0 1.0
Fe 0.0 1.0 1.0
Fe 1.0 0.0 1.0
Fe 1.0 1.0 0.0
Fe 1.0 1.0 1.0
D.2. Creating a "Body-Centered" Cubic Lattice
[5]
Finish create_BCC to return a CubicLattice
that has the same properties as a simple cubic (SC) lattice, with
the addition of a single Atom at the center of the crystal.
>>> from lattice_client import *
>>> ex_scc = create_SC('Fe', 1.0)
>>> for atom in ex_scc.atoms:
... print(atom) # 8 corners
...
Fe 0.0 0.0 0.0
Fe 1.0 0.0 0.0
Fe 0.0 1.0 0.0
Fe 0.0 0.0 1.0
Fe 0.0 1.0 1.0
Fe 1.0 0.0 1.0
Fe 1.0 1.0 0.0
Fe 1.0 1.0 1.0
>>> ex_bcc = create_BCC('Fe', 1.0)
>>> for atom in ex_bcc.atoms:
... print(atom) # 8 corners, 1 cell center
...
Fe 0.0 0.0 0.0
Fe 1.0 0.0 0.0
Fe 0.0 1.0 0.0
Fe 0.0 0.0 1.0
Fe 0.0 1.0 1.0
Fe 1.0 0.0 1.0
Fe 1.0 1.0 0.0
Fe 1.0 1.0 1.0
Fe 0.5 0.5 0.5
D.3. Creating a "Face-Centered" Cubic Lattice
[5-10]
Finish create_FCC to return a CubicLattice that has the same properties as
a simple cubic (SC) lattice, along with Atoms at each of the 6 faces of the cubic lattice.
Hint: The list of atoms you'll need to pass to the returned CubicLattice
should contain 8 corner atoms + 6 face atoms, appropriately positioned.
>>> from lattice_client import *
>>> ex_scc = create_SC('Fe', 1.0)
>>> for atom in ex_scc.atoms:
... print(atom) # 8 corners
...
Fe 0.0 0.0 0.0
Fe 1.0 0.0 0.0
Fe 0.0 1.0 0.0
Fe 0.0 0.0 1.0
Fe 0.0 1.0 1.0
Fe 1.0 0.0 1.0
Fe 1.0 1.0 0.0
Fe 1.0 1.0 1.0
>>> ex_fcc1 = create_FCC('Fe', 1.0)
>>> for atom in ex_fcc1.atoms:
... print(atom) # 8 corners, 6 faces
Fe 0.0 0.0 0.0
Fe 1.0 0.0 0.0
Fe 0.0 1.0 0.0
Fe 0.0 0.0 1.0
Fe 0.0 1.0 1.0
Fe 1.0 0.0 1.0
Fe 1.0 1.0 0.0
Fe 1.0 1.0 1.0
Fe 0.5 0.5 0.0
Fe 0.5 0.0 0.5
Fe 0.0 0.5 0.5
Fe 1.0 0.5 0.5
Fe 0.5 1.0 0.5
Fe 0.5 0.5 1.0
>>> ex_fcc4 = create_FCC('Al', 4.0) # changing to 4.0
>>> for atom in ex_fcc4.atoms:
... print(atom) # 8 corners, 6 faces
Al 0.0 0.0 0.0
Al 4.0 0.0 0.0
Al 0.0 4.0 0.0
Al 0.0 0.0 4.0
Al 0.0 4.0 4.0
Al 4.0 0.0 4.0
Al 4.0 4.0 0.0
Al 4.0 4.0 4.0
Al 2.0 2.0 0.0
Al 2.0 0.0 2.0
Al 0.0 2.0 2.0
Al 4.0 2.0 2.0
Al 2.0 4.0 2.0
Al 2.0 2.0 4.0
The best way to check whether you made the right lattice is to visualize! Upload your file to the .xyz file viewer (http://calistry.org/calculate/xyzviewer), where you should be able to see the location of each of your atoms!